π, a letter of the Greek alphabet used in mathematics to denote a particular irrational number—the ratio of the circumferenceto the diameter of a circle. The symbol was probably adopted from the Greek word for “circumference,” or “periphery.”Although it came into general use after a paper by L. Euler in 1736, it was first used by the British mathematician W. Jones in1706. Like all irrational numbers, π is an infinite nonrepeating decimal fraction:
π = 3.141592653589793238462643…
The requirements of practical calculations involving circles and circular solids long ago made it necessary to findapproximations of π by rational numbers. In the second millennium B.C., ancient Egyptian computations of the area of a circlemade use of the approximation π ≈ 3, or, more precisely, π ≈ (16/9)2= 3.16049.… In the third century B.C., Archimedes found,by comparing the circumference of a circle to regular inscribed and circumscribed polygons, that π is between the values
The second value is still used in calculations that do not require great accuracy. In the second half of the fifth century, theChinese mathematician Tsu Ch’ung-chih obtained the approximation 3.1415927, which much later (16th century) was alsofound in Europe. This approximation is exact for the first six decimal places.
The search for a more exact approximation of π continued in later periods. For example, in the first half of the 15th century,al-Kashi calculated π to 17 places. In the early 17th century, the Dutch mathematician Ludolph van Ceulen obtained 32places. For practical needs, however, it is sufficient to have values for π and the simplest expressions in which π occurs toonly a few decimal places; reference works usually give four- to seven-place approximations for π, 1/π, π2, and log π.
The number π appears not only in the solution of geometric problems. Since the time of F. Vieta (16th century), the limits ofcertain arithmetic sequences generated by simple rules have been known to involve π. An example is Leibniz’ series (1673-74)
This series converges extremely slowly. There exist series for calculating π that converge much more rapidly. An example isthe formula
where the values of the arc tangents are calculated by means of the series
The formula was used in 1962 for a computer calculation of π to 100,000 places. This type of calculation is of interest inconnection with the concept of random and pseudorandom numbers. Statistical processing has shown that this set of100,000 digits exhibits many features of a random sequence.
The possibility of a
purely analytic definition of π is of
fundamental importance for geometry. Thus, in
non-Euclideangeometry π also occurs in
some formulas but is no
longer the ratio of
the circumference to
the diameter of a
circle, for theratio is
not a
constant in
non-Euclidean geometry. The arithmetic nature of
π was finally clarified by
analytic means, amongwhich a
crucial role was played by
the remarkable Euler formula e2πi = 1,
where e is
the base of
the natural system of
logarithms and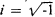 
.
At the end of the 18th century, J. H. Lambert and A. M. Legendre proved that π is irrational. In 1882 the Germanmathematician F. Lindemann showed it to be transcendental—that is, it cannot satisfy any algebraic equation with integralcoefficients. The Lindemann theorem conclusively established that the problem of squaring the circle cannot be solved bymeans of a compass and straightedge.
Special fact on Pi
The birthday of pi is also celebrated on 14th of march as pi day.
Pi is irrational no. it can never be end,
Proof
It is still after.
Let's suppose √2 is a rational number. Then we can write it √2 = a/b where a, b are whole numbers, b not zero.
